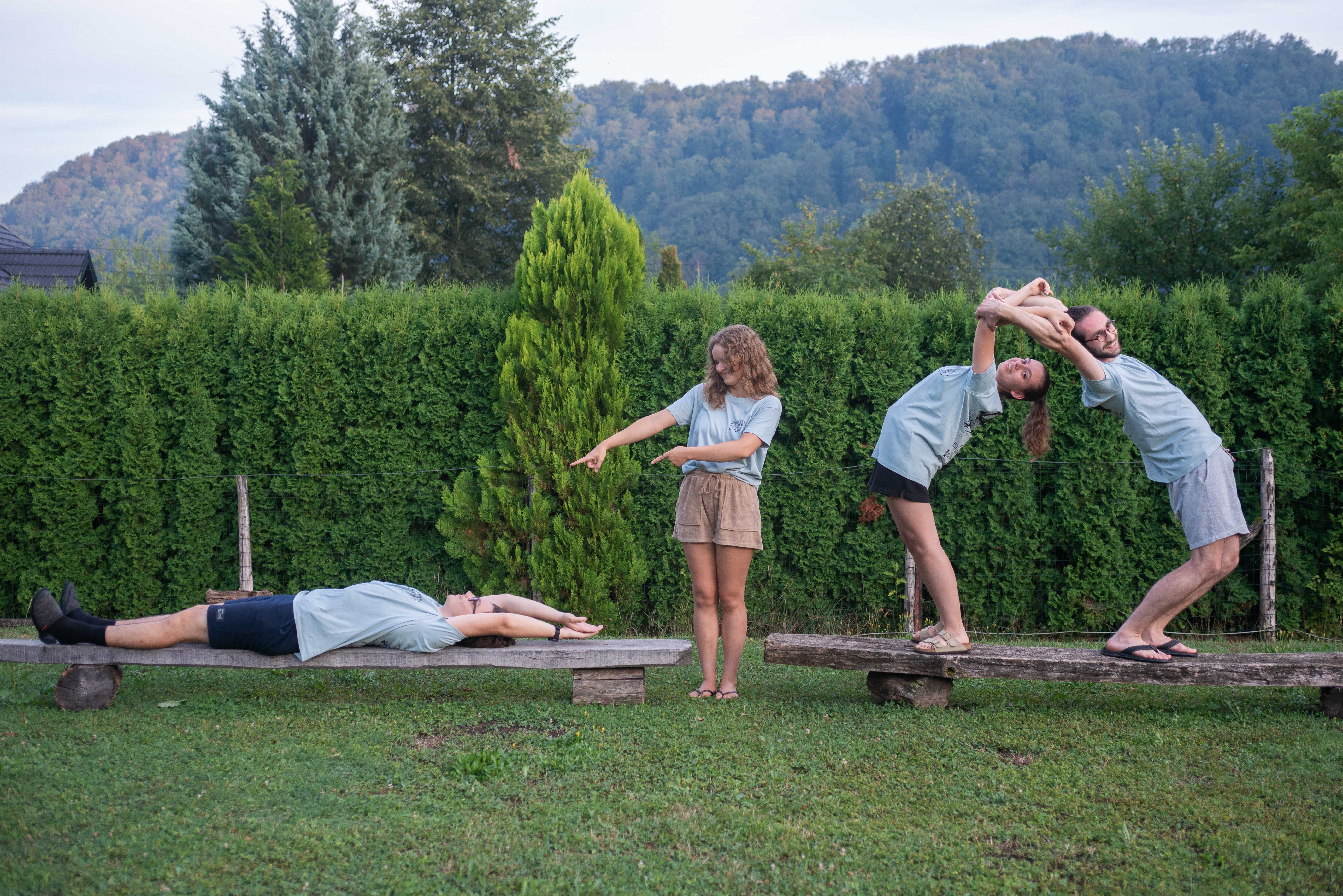MaRSovci vsako leto v skupinah pripravijo projekt, ki ga na koncu predstavijo. Letošnji projekti so prikazani spodaj, povzetke vseh dosedanjih MaRSovskih projektov pa lahko najdete tu.
Gnetenje prostorov
Lenart Dolinar, Gimnazija Bežigrad
Katarina Grilj, Srednja šola Slovenska Bistrica
Luka Peruš, Gimnazija Ravne na Koroškem
Mentor:
Katarina Šipec, FMF, Univerza v Ljubljani
V članku sta definirani topologija in homotopija ter predstavljeni primeri homotopije. Definirana je retrakcija in dokazana ekvivalenca med obstojem retrakcije diska na sfero in kontraktibilnostjo krožnice ter predstavljena razlika med šibkim in krepkim deformacijskim retraktom.
Štetje preko neskončnosti
Avtorji projekta: Zara Barbarić,
Gimnazija Bežigrad Nika Bogataj
Golc,
Gimnazija Kranj Tina Tiara
Opalič,
I. gimnazija v Celju Mentor: Nejc Zajc,
FMF, Univerza v Ljubljani
Spraševali smo se, kako šteti dlje od neskončnosti, zato smo se v projektu
posvetili ordinalnim številom. Zanje smo definirali računske
operacije in si ogledali pravila za računanje z njimi.
Avtorji projekta: Juš Kocutar,
II. gimnazija Maribor Matej Knap,
Gimnazija Bežigrad Kaja Rajter,
II. gimnazija Maribor Mentor: David Opalič,
ETH Zürich
Vsako oglišče d-dimenzionalne kocke želi poslati paket v neko ciljno
oglišče. Predstavimo determinističen algoritem in izpostavimo primere, v
katerih je počasen. Z dodajanjem naključnega koraka ga ''pohitrimo'' in to
dokažemo.
Nives Gošnjak,
Splošna Gimnazija Velenje Samo Krejan,
Gimnazija Bežigrad Hugo
Trebše,
Gimnazija Bežigrad Mentor:
Pri projektu smo se spoznali z osnovami kriptografije in abstraktne algebre
in ugotovili, da nam varnost pri kodiranju zagotavljajo dekodirni ključi in
ne algoritmi. Pogledali smo si različne šifre in napade
nanje, kako deluje Diffie-Hellmanova shema ter ElGamalov digitalni
podpis in napad nanj.
Avtorji projekta: Miha Brvar,
Gimnazija Bežigrad Manca Ernst,
I. gimnazija v Celju Tjaša
Gregorič,
Gimnazija Ledina Mentor: Izak Jenko,
FMF, Univerza v Ljubljani
Ukvarjali se bomo z Möbiusovimi transformacijami. To so preslikave
v kompleksni ravnini s točko v neskončnosti, ki ohranjajo krožnice
in premice. Obravnavali bomo tudi stereografsko projekcijo, ki slika
točke s sfere na ravnino.
Avtorji projekta: Domen Klopčič,
Srednja šola Domžale Kanisaja Nika
Kovačič,
Gimnazija Poljane Adam Rakun,
Gimnazija Ledina Mentor: Jakob Svetina,
FMF, Univerza v Ljubljani
Ali ste vedeli, da računalnik ni samo za igranje igric? V našem
projektu smo ugotovili, da je lahko zelo priročen pripomoček za matematike,
saj lahko namesto nas opravi težko delo. Zato smo napisali
nekaj algoritmov, po katerih nam računalnik najde rešitve nelinearnih
enačb (in to s čisto majhno napako).
Avtorji projekta: Kiana Petrič,
Waldorfska šola Ljubljana Nejc Ocepek,
Gimnazija Šiška Timotej Vičar,
Gimnazija Vič Mentor: Žan Hafner
Petrovski
V članku se spoznamo z osnovno metodo strojnega učenja, to je z linearno
regresijo. Pri tem postopku želimo znanim podatkom prirediti čim bolj
prilegajočo se premico, za izpeljavo njenega predpisa pa potrebujemo odvod.
Prek znanega pojma naklona premice spoznamo njegov geometrijski pomen, ki
nam koristi pri razumevanju iskanja ekstremov odvedljivih funkcij - taka pa
je tudi funkcija cene regresijske premice, ki v svojem minimumu določi oba
koeficienta premice.
Avtorji projekta: Matic Bratina,
Gimnazija Koper Eva Bračun,
Gimnazija Kranj Živa Kovačič,
II. gimnazija Maribor Mentor: Bor Grošelj
Simić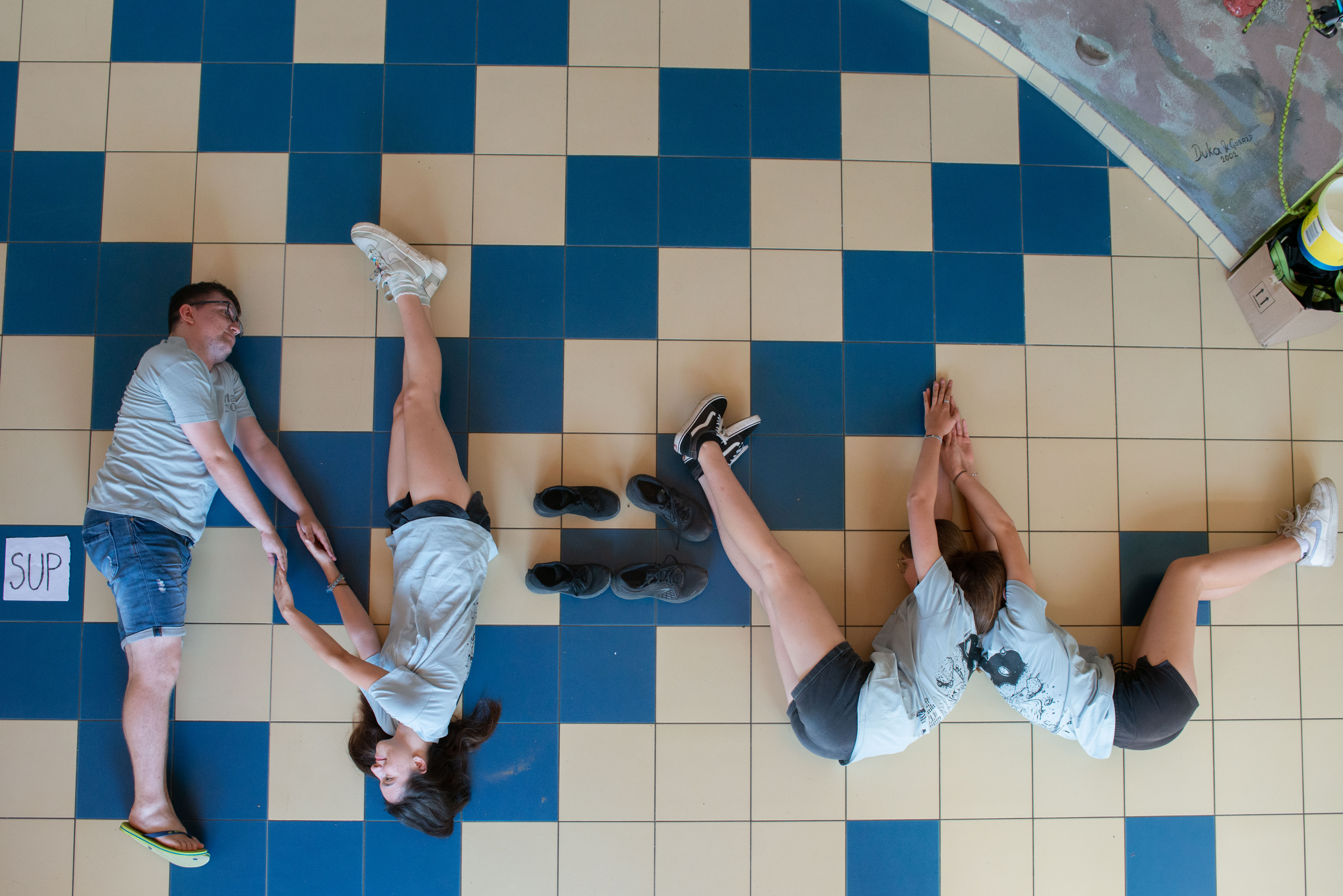
Pošiljanje paketov po d-dimenzionalni kocki
Osnove kriptografije in ElGamalov digitalni podpis
Nino
Cajnkar, FMF, Univerza v Ljubljani
Möbiusove transformacije
Numerično reševanje nelinearnih enačb
Linearna regresija
Ravninski grafi