MaRSovski projekti 2012

Avtor fotografij je Jan Šuntajs.

Pravična delitev

Avtorji projekta: Vesna Iršič, Gimnazija Bežigrad, Ljubljana Tilen Lučovnik, Gimnazija Vič, Ljubljana Simon Weiss, Gimnazija Bežigrad, Ljubljana Mentor: David Gajser, FMF, Univerza v Ljubljani Članek Ljudje se že od nekdaj srečujemo s problemom pravične delitve (na primer delitev torte ali predmetov med dediče). Pri projektu smo se ukvarjali s tem, kako razdeliti predmete, da bo volk sit in koza cela.

Celoštevilsko linearno programiranje

Avtorji projekta: Uroš Hekić, Gimnazija Ptuj, Ptuj Ana Reberc, II. gimnazija Maribor, Maribor Jasna Urbančič, Gimnazija Vič, Ljubljana Mentor: David Gajser, FMF, Univerza v Ljubljani Članek Sudoku (py)* * Za izvajanje je potreben modul PuLP. Naša skupina je najprej poskrbela za pripravo uravnoteženega mačjega obroka, nato pa poiskala način za avtomatsko reševanje sudokuja. Namesto lastnikov mačk lahko sudoku sedaj reši računalnik, mačke pa tako dobijo vso potrebno pozornost. Mijav.

Lov na komete

Avtorji projekta: Enej Bole, Gimnazija Koper, Koper Maja Furlan, Gimnazija Koper, Koper Erik Scheriani, United World College of the Adriatic, Devin (Italija) Mentor: Matej Aleksandrov, FMF, Univerza v Ljubljani Članek Demonstracija (ggb) Marsovci smo opazovali nebo in se odločili, da bomo določili orbite kometov. Prolema pa se nismo lotili numerično temveč s projektivno geometrijo. Uporabili smo zanimive lastnosti le-te, kot na primer premica v neskončnosti, princip dualnosti, Pascalov in Brianchonov izrek itd.

Marsovec v hribih

Avtorice projekta: Mateja Čarman, Srednja vzgojiteljska šola in gimnazija, Ljubljana Špela Pušnik, Šolski center Velenje – Umetniška gimnazija, Velenje Tisa Ževart, Šolski center Slovenj Gradec – Gimnazija, Slovenj Gradec Mentor: Jaka Špeh, FMF, Univerza v Ljubljani Članek Predstavljajte si pridnega Marsovca na poti v hribe, ki si zapisuje čase, ko doseže neko nadmorsko višino. Ker to lahko stori le ob določenih časih, ko ob poti opazi oznako, nima veliko meritev. Dobljene točke bi rad povezal s krivuljo. Mi smo se tega problema lotili z interpolacijo polinomov.

Mrežni mnogokotniki

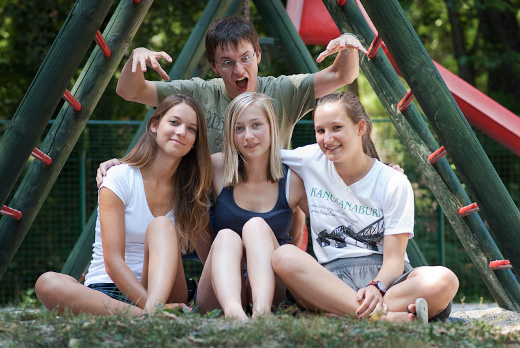
Avtorice projekta: Tjaša Košenina, I. gimnazija v Celju, Celje Klara Nosan, I. gimnazija v Celju, Celje Eva Zmazek, Gimnazija Ptuj, Ptuj Mentor: Nejc Rosenstein, FMF, Univerza v Ljubljani Članek V članku smo preverili, ali je mogoče v celoštevilsko kvadratno mrežo vrisati mnogokotnik na tak način, da njegova oglišča ležijo na točkah mreže. Nadalje smo preverili še, katere pravilne mnogokotnike lahko na tak način vrišemo v preprosto kubično celoštevilsko mrežo.

Tibetanska meniha

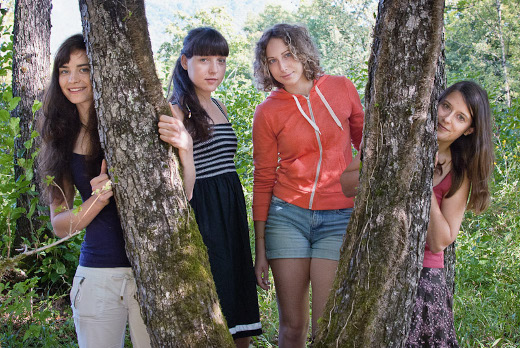
Avtorice projekta: Sara Pia Marinček, Gimnazija Bežigrad, Ljubljana Nadja Ogrinc, I. gimnazija v Celju, Celje Anja Petković, Gimnazija Bežigrad, Ljubljana Mentorica: Maja Alif, FMF, Univerza v Ljubljani Članek Demonstracija (html) Meniha plezata čez Himalajo tako, da prideta vsak na drugo stran gorovja. Ves čas vzpona morata biti na istih nadmorskih višinah. S pomočjo teorije grafov se dokaže, da jima to lahko uspe. Definira se graf, katerega vozlišča so urejeni pari točk z isto nadmorsko višino, od katerih je vsaj ena prelomna. Nato se poišče pot med začetnim in končnim vozliščem in tako pokaže, da je tak vzpon res mogoč.

Peanova krivulja

Avtorice projekta: Tjaša Bajc, Gimnazija Poljane, Ljubljana Ana Smerdu, Gimnazija Poljane, Ljubljana Živa Urbančič, Gimnazija Vič, Ljubljana Mentorica: Jana Vidrih, FMF, Univerza v Ljubljani Članek Demonstracija (html) Peanova krivulja je zvezna surjektivna preslikava enotskega intervala v enotski kvadrat. Obstajajo veliko različnih krivulj s takimi lastnostmi, mi pa smo se posvetili eni od enostavnejših. Opisali bomo konstrukcijo krivulje in nekaj njenih zanimivih lastnosti.

Vigenèrjeva šifra

Avtorji projekta: Alenka Bahovec, Škofijska klasična gimnazija, Ljubljana Rok Kaufman, Gimnazija Vič, Ljubljana Vid Kocijan, Gimnazija Vič, Ljubljana Mentor: Matej Roškarič, FNM, Univerza v Mariboru Članek Demonstracija (zip) Vigenèrjeva šifra je postopek šifriranja, ki je ostal nerazbit skoraj štiristo let. Predstavili bomo njene lastnosti, zgodovino uporabe in računalniški program, ki jo razbije.